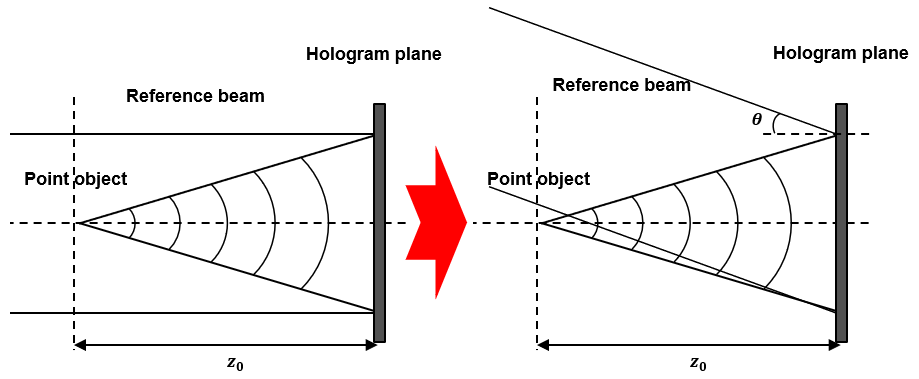
This module is related method which convert to off-axis hologram.
Introduction
- Complex hologram records the amplitude and the complete phase of the diffracted optical field, reconstr uction of the complex hologram can give the 3D image of an object without the twin-image and background noise [1]. However, a conventional SLM cannot represent a complex hologram because the SLM can represent either amplitude or phase. Because a conventional amplitude-only SLM can modulate the amplitude of an opti cal field, we can represent either the real or the imaginary part of the complex hologram with DC bias. However, when we reconstruct the 3D image of the object optically for 3D display using an amplitude-only SLM, the reconstructed 3D image of the object is corrupted by the twin-image and background noise. On the other hand, a phase-only SLM modulates only the phase of an optical field, and, thus, if we represent the phase of the comp lex hologram using the phase-only SLM, the reconstructed 3D image is distorted by amplitude flattening.
- Convert complex holograms into off-axis holograms, which can reconstruct 3D images of objects without distor tion due to twin image noise, background noise, and amplitude flattening [4].
Algorithm
- In the off-axis hologram, the optical axis of the reference wave is tilted to that of the object wave. The angle between the optical axes of the reference and object waves introduces a spatial carrier within the hologram. The spatial carrier allows the separation of the desired 3D image of the object from the twin-image noise and background noise in the reconstruction stage[2,3]. To convert the complex hologram to an off-axis hologram, we multiply a spatial carrier term to complex hologram, \( H_{complex} \)
\[ H_{complex}^{spatial carrier}(x,y)= \left | H_{complex} \right | \exp \left ( j \angle H_{complex}\right ) \exp \left (j\frac{2\pi\sin\theta}{\lambda}x \right ) = \left | H \right | \exp\left[j\left( \angle H_{complex}+\frac{2\pi\sin\theta}{\lambda}x\right ) \right] \qquad \left(1\right) \]
- where \(\angle\) represents the phase of a complex function, and \(\theta\) is a tilted angle between the optical axes of the reference and object waves. Note that we need to choose the off-axis angle, \(\theta\), large enough to sepa rate the desired 3D image from the twin-image and background noise[2,3]. The spatial carrier that is added to the complex hologram separates the background noise as the zeroth-order beam and the twin image as the first-order beam, which are spatially separated from the desired 3D image in the optical reconstr uction[2,3]. To acquire an off-axis real hologram suitable for display on an amplitude-only SLM, we extract the real part of Eq. (1) and add a DC bias to give
\[ H_{complex}^{off-axis}(x,y) =Re\left[H_{complex}^{spatialcarrier}(x,y)\right]+dc =\left|H_{complex}^{spatialcarrier}(x,y)\right|\cos\left(\angle H_{complex}+\frac{2\pi\sin\theta}{\lambda} x\right)+dc \qquad \left(2\right) \]
- where dc is a DC bias added to make the off-axis hologram become a positive value.
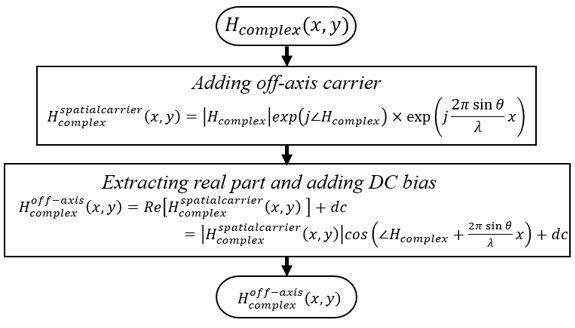
Figure 2. Flowchart
Reference
- [1] T.-C. Poon, T. Kim, G. Indebetouw, B. W. Schilling, M. H. Wu, K. Shinoda, and Y. Suzuki, “Twin-image elimination experiments for three-dimensional images in optical scanning holography,” Opt. Lett. 25, 215–217 (2000).
- [2] E. N. Leith and J. Upatnieks, “Reconstructed wavefronts and communication theory,” J. Opt. Soc. Am. 52, 1123–1130 (1962). 16.
- [3] E. N. Leith and J. Upatnieks, “Wavefront reconstruction with continuous-tone objects,” J. Opt. Soc. Am. 53, 1377–1381 (1963).
- [4] Y. S. Kim, T. Kim, T.-C. Poon, and J. T. Kim, “Three-dimensional display of a horizontal-parallax-only hologram,” Applied Optics Vol. 50, Issue 7, pp. B81-B87 (2011)
◆ sigConvertOffaxis()
| bool ophSig::sigConvertOffaxis |
( |
Real |
angleX, |
|
|
Real |
angleY |
|
) |
| |
Function for Convert complex hologram to off-axis hologram.
- Parameters
-
| angleX | X-axis angle of off-axis |
| angleY | Y-axis angle of off-axis |
- Returns
- if works well return 0 or error occurs return -1
Definition at line 996 of file ophSig.cpp.
◆ sigConvertOffaxis_CPU()
| bool ophSig::sigConvertOffaxis_CPU |
( |
Real |
angleX, |
|
|
Real |
angleY |
|
) |
| |
|
protected |
Function for Convert complex hologram to off-axis hologram by using CPU.
- Parameters
-
| angleX | X-axis angle of off-axis |
| angleY | Y-axis angle of off-axis |
- Returns
- if works well return 0 or error occurs return -1
◆ sigConvertOffaxis_GPU()
| bool ophSig::sigConvertOffaxis_GPU |
( |
Real |
angleX, |
|
|
Real |
angleY |
|
) |
| |
|
protected |
Function for Convert complex hologram to off-axis hologram by using GPU.
- Parameters
-
| angleX | X-axis angle of off-axis |
| angleY | Y-axis angle of off-axis |
- Returns
- if works well return 0 or error occurs return -1