Point Cloud

Collaboration diagram for Point Cloud:

Classes
class	ophPointCloud
	Openholo Point Cloud based Compter-generated holography. More...

Detailed Description

Introduction

This module is related methods which generates CGH based on 3D point cloud. It is supported single core processing, multi-core processing(with OpenMP) and GPGPU parallel processing(with CUDA).

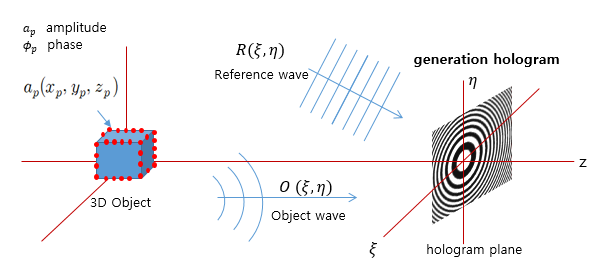
-Fig1.Hologram generation by object beam and reference beam

I. Point Cloud Hologram Generation with Rayleigh-Sommerfeld(RS) Integral

Reference wave :

\[ R \left( \xi,\eta \right) = a_{R} \exp \left\{ -jk \left( \xi \sin \theta_{\xi} + \eta \sin \theta_{\eta} \right) \right\} \]

Object wave :

\[ O \left( \xi,\eta \right) = \sum_{p=1}^{N} \frac{a_{p}}{r_{p}} \exp \left\{ j \left( kr_{p} + \phi_{p} \right) \right\} \]

Distance :

\[ r_{p} = \sqrt{ \left( \xi - x_{p} \right)^{2} + \left( \eta - y_{p} \right)^{2} + z_{p}^{2} } \]

Intensity :

As shown in Fig. 1, when the object wave and the reference wave are overlapped with each other, an interference pattern is generated by each other.
Therefore, the interference pattern of the hologram plate The intensity, I, is:

\[ I \left( \xi,\eta \right) = \left| O \left( \xi,\eta \right) + R \left( \xi,\eta \right) \right|^{2} = \left| O \right|^{2} + \left| R \right|^{2} + R^{*} O + R O^{*} \]

Since the \(\left|O\right|^{2} + \left|R\right|^{2}\) in this case does not have three-dimensional information as a DC term, it is not used, and \(R^{*}O + RO^{*}\), which is the following two terms, has hologram information.

The interference pattern generated on the hologram is calculated by the interference between the object wave and the reference wave as in the above equation.
Here, the \(\left|O\right|^{2} + \left|R\right|^{2}\) formula is the intensity distribution of the object wave and the reference wave, which is irrelevant to the image of the object, but the \(R^{*}O + RO^{*}\) formula has the hologram information of the object.
When calculating the interference pattern, Only a simplified calculation can be performed. If you select this port and calculate it briefly, you will get the following formula.

\[ I \left( \xi,\eta \right) = \sum_{i=1}^{N} \frac{a_{i}}{r_{i}} \exp \left( kr_{i} + k \xi \sin \theta_{\xi} + k \eta \sin \theta_{\eta} \right) \]

II. Point Cloud Hologram Generation with Rayleigh-Sommerfeld(RS) Integral 2

Rayleigh-Sommerfeld solution I :

\[ u \left( x,y \right) = \frac{z}{j \lambda} \int_{}^{} { \int_{\Sigma}^{} {u \left( \xi,\eta \right) \frac{ \exp \left( jkr_{01} \right) } {r_{01}^{2}} } d \xi } d \eta \]

Impulse response

\[ h \left( x,y \right) = \frac{z}{j \lambda} \frac{ \exp \left( jkr \right) }{r^{2}} \]

R-S diffraction Anti-alliasing

\[ \frac{1}{2\pi} \left| \frac{\partial \phi}{\partial x} \right| < \frac{1}{2 p_{x}} ,\quad \frac{1}{2\pi} \left| \frac{\partial \phi}{\partial y} \right| < \frac{1}{2 p_{y}} \qquad \to \qquad \frac{1}{2\pi} \left| \frac{x - x_{o}}{r} \right| < \frac{1}{2 p_{x}} ,\quad \frac{1}{2\pi} \left| \frac{y - y_{o}}{r} \right| < \frac{1}{2 p_{y}} \]

\[ \to \qquad \begin{matrix} x_{o} - \left| \frac{t_{x}}{\sqrt{1 - t_{x}^{2}}} \sqrt{ \left( y - y_{o}^{2} \right) + z_{o}^{2} } \right| \quad < \quad x \quad < \quad x_{o} + \left| \frac{t_{x}}{\sqrt{1 - t_{x}^{2}}} \sqrt{ \left( y - y_{o}^{2} \right) + z_{o}^{2} } \right| ,\\ y_{o} - \left| \frac{t_{y}}{\sqrt{1 - t_{y}^{2}}} \sqrt{ \left( x - x_{o}^{2} \right) + z_{o}^{2} } \right| \quad < \quad y \quad < \quad y_{o} + \left| \frac{t_{y}}{\sqrt{1 - t_{y}^{2}}} \sqrt{ \left( x - x_{o}^{2} \right) + z_{o}^{2} } \right| \end{matrix} \]

\[ \texttt{where} \quad t_{x} = \frac{\lambda}{2p_{x}} ,\quad t_{y} = \frac{\lambda}{2p_{y}} \]

Search Range : Rectangle

\[ \texttt{x direction} \quad \to \quad y = y_{o} \quad \to \quad x_{o} - \left| \frac{t_{x}}{\sqrt{1 - t_{x}^{2}}} z_{o} \right|\ <\ x\ <\ x_{o} + \left| \frac{t_{x}}{\sqrt{1 - t_{x}^{2}}} z_{o} \right| \]

\[ \texttt{y direction} \quad \to \quad x = x_{o} \quad \to \quad y_{o} - \left| \frac{t_{y}}{\sqrt{1 - t_{y}^{2}}} z_{o} \right|\ <\ y\ <\ y_{o} + \left| \frac{t_{y}}{\sqrt{1 - t_{y}^{2}}} z_{o} \right| \]

III. Point Cloud Hologram Generation with Fresnel Diffraction Integral

Fresnel Diffraction Integral :

\[ u \left( x,y \right) = \frac{z}{j \lambda} \int_{}^{} { \int_{}^{} { u \left( \xi,\eta \right) \frac{ \exp \left( jkr_{01} \right) } {r_{01}^{2}} } d \xi } d \eta \cong \frac{e^{jkz}}{j \lambda z} \int_{}^{} { \int_{}^{} { u \left( \xi,\eta \right) \exp \left\{ j \frac{k}{2z} \left[ \left( x - \xi \right)^{2} + \left( y - \eta \right)^{2} \right] \right\} } d \xi } d \eta \]

Impulse response

\[ h \left( x,y \right) \cong \frac{e^{jkz}}{j \lambda z} \exp \left\{ j \frac{k}{2z} \left( x^{2} + y^{2} \right) \right\} \]

Fresnel diffraction Anti-alliasing

\[ \begin{matrix} \frac{1}{2\pi} \left| \frac{\partial \phi}{\partial x} \right| < \frac{1}{2 p_{x}} ,\\ \frac{1}{2\pi} \left| \frac{\partial \phi}{\partial y} \right| < \frac{1}{2 p_{y}} \end{matrix} \qquad \to \qquad \begin{matrix} x_{o} - \left| \frac{\lambda z_{o}}{2 p_{x}} \right|\ <\ x\ <\ x_{o} + \left| \frac{\lambda z_{o}}{2 p_{x}} \right| ,\\ y_{o} - \left| \frac{\lambda z_{o}}{2 p_{y}} \right|\ <\ y\ <\ y_{o} + \left| \frac{\lambda z_{o}}{2 p_{y}} \right| \end{matrix} \]